《机械基础》专升本考试大纲怀化学院

一、课程基本信息

本课程是机械专业的专业必修课，让学生联系实际进行理论学习，让学生掌握机械基础知识，同时培养学生的机械分析能力，为这些专业的学生学习后续专业课程，提供一个专业基础知识平台。课程主要包括三大部分：工程材料及热处理、机械原理与设计、公差与配合。

二、课程考试目的

通过本课程的考试，以检验学生对机械技术的基本知识和基本技能的掌握程度，考核学生分析机械的功能、动作及应用一般机械能力的初步具备程度。

三、考试内容与要求

第一部分 工程材料及热处理

第一章 铁碳合金材料

考核要点：

1、 能看懂铁碳合金相图，准确地说出相图中特征点线的含意，并根据相图判断常温下合金的金相组织结构;

2、了解钢的分类，准确理解钢的牌号，机械零件常用钢的性能及用途，以及Q215、Z45、65Mn、20Mn钢等结构钢的用途，了解牌号9SiCr、W18Cr4V、YG6X、YT30等工具钢的用途;

3、能够识读铸铁的牌号，了解铸铁的种类，了解铸铁的用途。

第二章 铝及铝合金

考核要点：

1、识读铝合金的牌号和用途;

2、形变铝合金的工艺性能。

第三章 热处理

考核要点：

1、钢的热处理种类及应用场合;

2、35钢、65Mn钢、9SiCr的热处理方法及意义;

3、了解热处理后金相组织变化。

第二部分 机械原理及设计

第一章 平面四杆机构

考核要点：

1、运动副的概念、自由度的计算;

2、平面四杆机构的结构、种类;

3、极位夹角、急回特性、死点、压力角的概念。

第二章 齿轮机构

考核要点：

1、齿轮的种类及特点;

2、直齿圆柱齿轮的结构计算;

3、齿轮轮系的类型，定轴轮系传动比的计算。

第三章 螺纹连接及传动

考核要点：

1、螺纹的类型及用途、螺纹连接的类型;

2、普通螺纹的结构，标识;

3、螺栓连接的强度计算;

4、螺纹传动的应用。

第四章 轴系

考核要点：

1、轴的常用材料及热处理;

2、轴的结构设计;

3、滚动轴承的结构，深沟球轴承、角接触球轴承、推力球轴承、圆锥滚子轴承的牌号和用途。

第三部分 公差配合

考核要点：

1、公差与配合的概念;

2、公差带图的应用与计算;

3、配合的种类及计算;

4、公差代号及标注，配合标识及应用。

四、考试方式与时间

考试方式：笔试，闭卷

考试时长：2小时

五、考试题型结构及分值分布

考试试卷总分100分。考试题型分为6大类： 1、填空题(15分);2、单项选择题(15分); 3、 判断题(15分);4、简答题(20分); 5、计算题 (23分) ;6、分析题(12分)

六、教材与参考书目

教材：《机械基础》第1版，杨明霞主编，北京理工大学出版社，2016.1

参考书目：

1、《机械基础教学参考书》第4版，孙大俊主编，中国劳动社会保障出版社，2007.9

2、《机械基础》刘跃男主编，高等教育出版社，2010.6

附录：题型举例

《机械制图》专升本考试大纲怀化学院

一、课程基本信息

机械制图是机械专业的专业基础能力必修课程。机械制图是机械设计制造的技术语言，是一门既有国家标准又有行业规范，既有系统理论又有较强实践性的专业基础课。课程包括画法几何的基础知识、工程制图标准、机械零件图、机械装配图表达等内容。通过本课程的学习，使学生具有初步绘制机械零件图和识读机械图样的能力，学习运用三视图、组合体投影规律、标准件与常用件的规定画法和标注方法等绘制机械产品，为后续专业学习提供交流工具和学习基础。

二、课程考试目的

通过本课程的考试，主要检验学生以下基本知识与能力的掌握程度：

1、掌握国家制图标准的概念，掌握工程制图的国家标准，掌握画法几何的点、线、面投影基础知识，掌握工程图三视图表达方法要点，掌握机械零件图的绘制要点，掌握机械装配图的绘制要点。

2、能够准确地识读和绘制机械零件、机构等工程图样;并具备初步的机械零件设计能力。

三、考试内容与要求

第一章 机械制图国家标准

考核要点：

1、图框、图线、字体、比例、尺寸标注规范;

2、标题栏及其表达;

3、第一角正投影规范。

第二章 基本体投影

考核要点：

1、点、线、面的平等正投影规则;

2、正棱柱、正棱锥、圆柱、圆锥、球的三面投影;

3、点与线的投影关系，两线投影关系，点线在面上的投影关系。

第三章 组合体表达

考核要点：

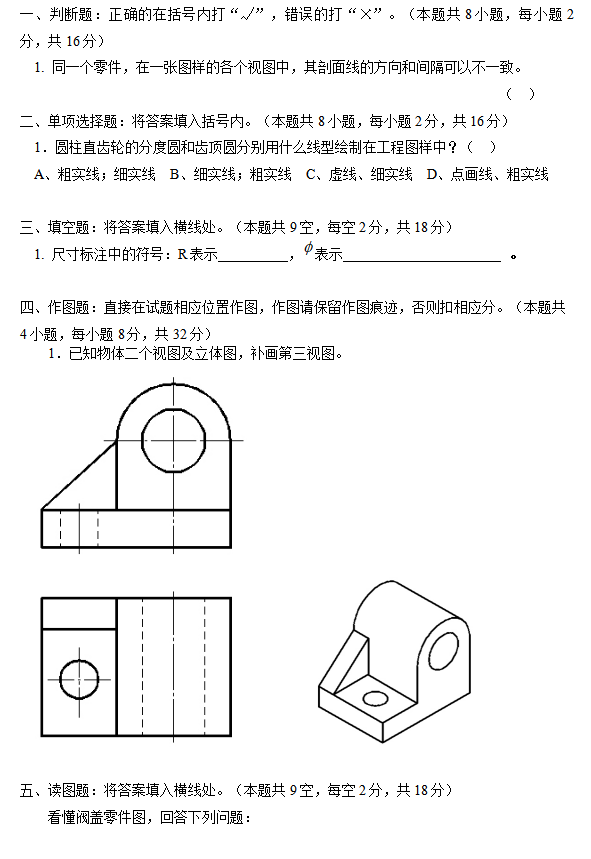
1、读三视图，补齐第三面视图，改正视图中的错误或漏线;

2、三视图尺寸标注;

3、由轴测图绘制工程图;

4、改变三视图的表达，改用剖视图表达。

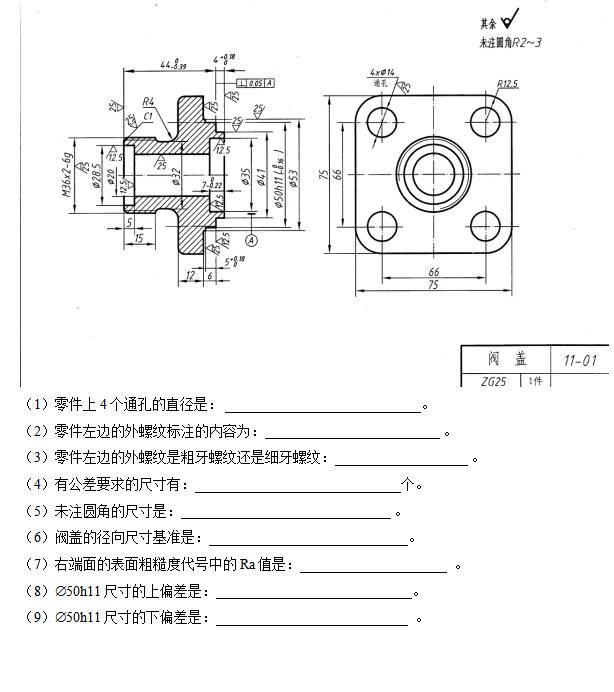
第四章 零件图

考核要点：

1、螺纹及螺纹配合的表达;

2、齿轮的表达;

3、轴承的规定画法;

4、识读典型零件，回答绘图问题。

第五章 装配图

考核要点：

1、读常见的机械装配图，拆给零件图;

2、读一般难度的装配图，回答工程图绘制知识问题。

四、考试方式与时间

考试方式：笔试，闭卷

考试时长：2小时

五、考试题型结构及分值分布

考试试卷总分100分。考试题型分为5大类： 1、判断题(16分);2、单项选择题(16分); 3、 填空题(18分);4、作图题(32分); 5、读图题(18分)

六、教材与参考书目

教材：《机械制图》，余晓琴、杨晓红等主编，机械工业出版社，2017.12

参考书目：

1、《画法几何及机械制图》 杨裕根主编，北京邮电大学出版社，2016.6

2、《机械制图》，仝基斌　晏群主编，机械工业出版社，2008.11

附录：题型举例

《高等数学》课程考试大纲

一、课程基本信息

1.课程性质：公共基础课

2.适用对象：怀化学院理、工、经、管类专业专升本招生考试

二、课程考试目的

《高等数学》课程考试旨在考察学生对微积分知识的掌握情况以及运用微积分知识解决实际问题的能力.

三、考试内容与要求

第一章 函数、极限与连续

(一)考试内容

一元函数的概念，函数的性质，反函数，基本初等函数的概念、性质及其图形，复合函数，初等函数，数列极限，函数极限，无穷小与无穷大，无穷小与极限之间的关系，无穷小与无穷大之间的关系，极限的运算法则，极限存在准则，两个重要极限，无穷小的比较，函数的连续性，函数的间断点及其分类，连续函数的运算定理，初等函数的连续性，闭区间上连续函数的基本性质.

(二)考试要求

1.理解函数、初等函数的概念;

2.了解函数的性质以及反函数的概念;

3.掌握基本初等函数的性质及其图形;

4.理解极限的概念，思想方法;

5.了解极限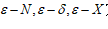的定义;

6.掌握左、右极限的概念，左、右极限与极限的关系;

7.掌握极限的四则运算法则;

8.了解两个极限存在准则，掌握两个重要极限;

9.理解无穷小的概念及与极限的关系;

10.了解无穷小的比较;

11.理解连续的两种定义，掌握连续性的证明方法、连续函数的运算性质，会判定间断点的类型;

12.理解闭区间上连续函数的性质，会用零点定理判别方程的根。

第二章 一元函数微分学

(一)考试内容

导数的概念，基本初等函数的导数，函数的和、差、积、商的导数，反函数和复合函数的导数，高阶导数，隐函数的导数，参数方程确定的函数的导数，微分的基本公式，微分形式不变性，微分在近似计算中的应用.

(二)考试要求

1.理解导数的概念，会利用概念求函数的导数;

2.掌握导数的几何意义，掌握求曲线的切线方程和法线方程的方法，了解可导与连续的关系;

3.掌握导数的运算;

4.理解微分的概念、几何意义、微分形式不变性，了解可导与可微的关系;

5.了解微分在近似计算中的应用;

第三章 一元函数微分学的应用

(一)考试内容

微分中值定理(罗尔定理、拉格朗日中值定理、柯西中值定理)，罗必塔法则，泰勒公式，函数单调性的判别，函数的凸凹性及拐点的判别，函数的极值概念及求法，最大值与最小值的求法及其应用，函数图形的水平渐近线与铅直渐近线的求法.

(二)考试要求

1.了解三个微分中值定理的条件、结论，能证明前两个定理，了解构造函数的方法，掌握不等式的证明;

2.掌握洛必达法则的条件、结论以及常见的各种未定式极限的计算;

3.掌握泰勒公式和麦克劳林公式展开某些较简单的初等函数并求其近似值;

4.掌握函数的单调性、凹凸性、拐点、极值点的判别方法，会求曲线的水平渐近线和铅直渐近线;

5.掌握解决函数的最大值、最小值的求法，并能应用于求解实际问题。

第四章 一元函数积分学

(一)考试内容

定积分的概念，定积分的基本性质，微积分的基本定理，原函数与不定积分的概念，不定积分的基本性质，基本积分公式，换元积分法，分部积分法，有理函数的积分，三角函数有理式的积分，定积分的计算。

(二)考试要求

1.理解定积分的概念，几何意义，掌握定积分的性质;

2. 理解不定积分的概念、性质，了解不定积分的几何意义;

3.掌握不定积分的基本积分公式，掌握不定积分的基本求法;

4.掌握不定积分的两类换元积分和分部积分法;

5.掌握简单的有理函数、三角函数有理式、无理式的积分的求法;

6.掌握定积分的换元积分法和分部积分法;

7.理解变上限的定积分作为其上限的函数及其求导定理，熟悉牛顿-莱布尼兹公式和变上限积分函数的求导;

第五章 一元函数积分学的应用

(一)考试内容

积分元素法，定积分在求平面图形面积、几何体体积、曲线弧长、做功等物理量中的应用.

(二)考试要求

1.掌握定积分的积分元素法;

2. 掌握用定积分求平面图形面积、几何体体积、曲线弧长的方法;

3. 了解做功、水压力的计算方法;

第六章 微分方程

(一)考试内容

微分方程基本概念，可分离变量方程，齐次方程，一阶线性微分方程.

(二)考试要求

1.了解微分方程、阶、解、通解、初始条件和特解等概念;

2.会识别下列几种一阶微分方程：变量可分离的方程，一阶线性方程，齐次方程;

3.掌握变量可分离方程及一阶线性方程的解法;

4.了解微分方程解决简单的几何问题和物理问题的方法。

第七章 向量与空间解析几何

(一)考试内容

空间直角坐标系，两点间距离公式，向量代数，直线、平面的方程，常见曲面及其方程.

(二)考试要求

1.了解空间直角坐标系，能建立空间点与数组的一一对应关系;

2.掌握两点间距离公式,了解向量的运算(线性运算、点乘法、叉乘法),掌握两个向量夹角的求法与垂直、平行的条件;

3.掌握利用坐标表达式进行向量运算的方法;

4.掌握平面、直线的方程及求法;

5.了解常见曲面的几何形状及方程。

第八章 多元函数微分学

(一)考试内容

二元函数的概念，二元函数的图像，二元函数的极限、连续，偏导数的概念，高阶偏导数、全增量与全微分，全微分存在的条件，多元复合函数微分法，隐函数及其微分法.

(二)考试要求

1.理解二元函数的概念，了解二元函数的几何意义;

2.了解二元函数的极限、连续性等概念以及有界闭域上连续二元函数的性质;

3.理解偏导数、全微分等概念并掌握其计算方法，了解全微分存在条件;

4.掌握复合函数的偏导数的求法;

5.掌握求隐函数所确定的函数的偏导数的方法;

第九章 多元函数微分学的应用

(一)考试内容

空间曲线的切线和法平面，空间曲面的切平面与法线，方向导数，二元函数的极值，最大值、最小值及其应用.

(二)考试要求

1.掌握空间曲线的切线和法平面、空间曲面的切平面与法线的求法;

2. 理解方向导数的概念;

3.理解多元函数极值的概念，会求函数的极值;

4. 了解条件极值的概念，会用拉格朗日乘数法求条件极值;

5.会求一些较简单的多元函数的最大值和最小值的应用问题。

第十章 多元函数积分学(I)

(一)考试内容

二重积分的概念及性质，二重积分的计算，二重积分的应用，对弧长的曲线积分，对面积的曲面积分。

(二)考试要求

1.理解二重积分的概念，了解二重积分的性质;

2.掌握直角坐标下二重积分的计算方法;

3.了解极坐标下二重积分的计算方法;

4.会应用二重积分求面积、体积、薄片质量;

5. 理解对弧长的曲线积分的定义和性质;

6. 掌握对弧长的曲线积分的计算方法;

7. 了解对面积的曲面积分的定义、性质和计算方法。

第十一章 多元函数积分学(II)

(一)考试内容

对坐标的曲线积分，对坐标的曲面积分;

(二)考试要求

1. 理解对坐标的曲线积分的定义和性质;

2. 掌握对坐标的曲线积分的计算方法;

3. 了解对坐标的曲面积分的定义、性质和计算方法。

四、考试方式及时间

1.考试方式：闭卷

2.考试时间：120分钟

五、考试题型结构及分值分布

1. 考试题型结构：单项选择题，填空题，判断题，计算题，证明题。

2. 分值分布(满分 100分)：

(1)单项选择题(每小题3分，共15分);

(2)填空题(每小题4分，共20分);

(3)判断题(每小题2分，共10分);

(4)计算题(每小题7分，共42分);

(5)证明题、综合题(共13分)，

六、教材与参考书目

1.高等数学(上)，黄立宏 主编，北京大学出版社， ISBN：9787301295045

2. 高等数学(下)，黄立宏 主编，北京大学出版社， ISBN：9787301295076

3. 高等数学(第七版)(上册)，同济大学应用数学系 编,高等教育出版社，ISBN：9787040396638.

4. 高等数学(第七版)(下册)，同济大学应用数学系 编,高等教育出版社，ISBN：9787040396621 .

怀化学院公共数学教研室

附 录(题型举例)

原网址：http://zsb.hhtc.edu.cn/info/1022/1945.htm